Linearity of Relation Decoding in Transformer LMs

Evan Hernandez1*, Arnab Sen Sharma2*, Tal Haklay3, Kevin Meng1, Martin Wattenberg4, Jacob Andreas1, Yonatan Belinkov3, David Bau2
1MIT CSAIL, 2Northeastern University, 3Technion - IIT; *Equal contribution

ArXiv Preprint thumbnail
ArXiv
Preprint Github code thumbnail
Source Code
 Dataset thumbnail
Dataset

How do Transformer LMs Decode Relations?

Much of the knowledge contained in neural language models may be expressed in terms of relations. For example, the fact that Miles Davis is a trumpet player can be written as a relation (plays the instrument ) connecting a subject (Miles Davis ) to an object (trumpet ).

One might expect how a language model decodes a relation to be a sequence of complex, non-linear computation spanning multiple layers. However, in this paper we show that for a subset of relations this (highly non-linear) decoding procedure can be well-approximated by a single linear transformation (LRE) on the subject representation s after some intermediate layer.

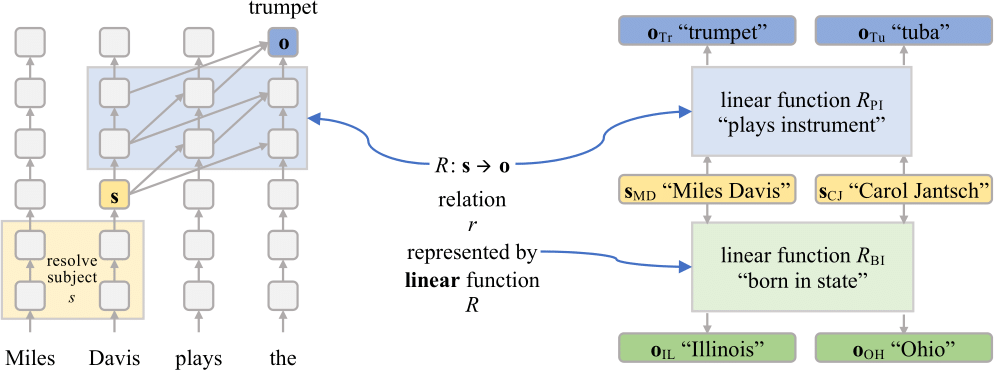
In an LM relations such as plays the instrument can be well-approximated by a linear function R that maps subject representation s to object representation o, which is then directy decoded.

How to get the LRE approximating a relation decoding?

A linear approximation in form of LRE(s) = Ws + b can be obtained by taking a first order Taylor series approximation to the LM computation, where W is the local derivative (Jacobian) of the LM computation at some subject representation s0. For a range of relations we find that averaging the estimation of LRE parameters on just 5 samples is enough to get a faithful approximation of LM decoding.

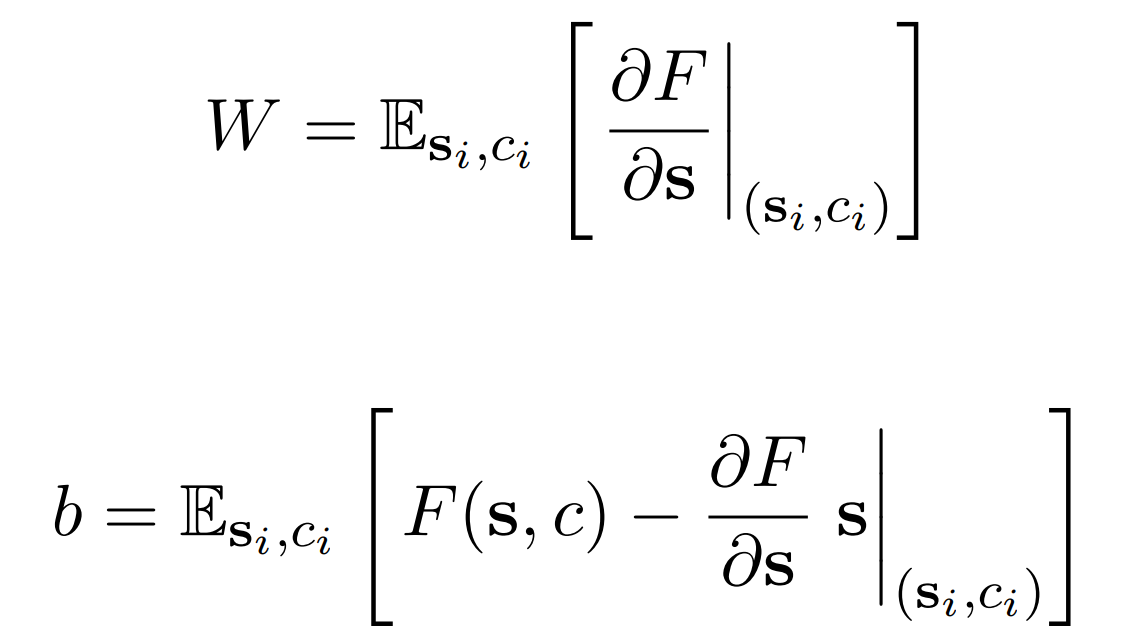
Here F represents how LM obtains the object representation o from the subject representation s introduced within a textual context c. Kindly refer to our paper for further details.

How good is the LRE approximation?

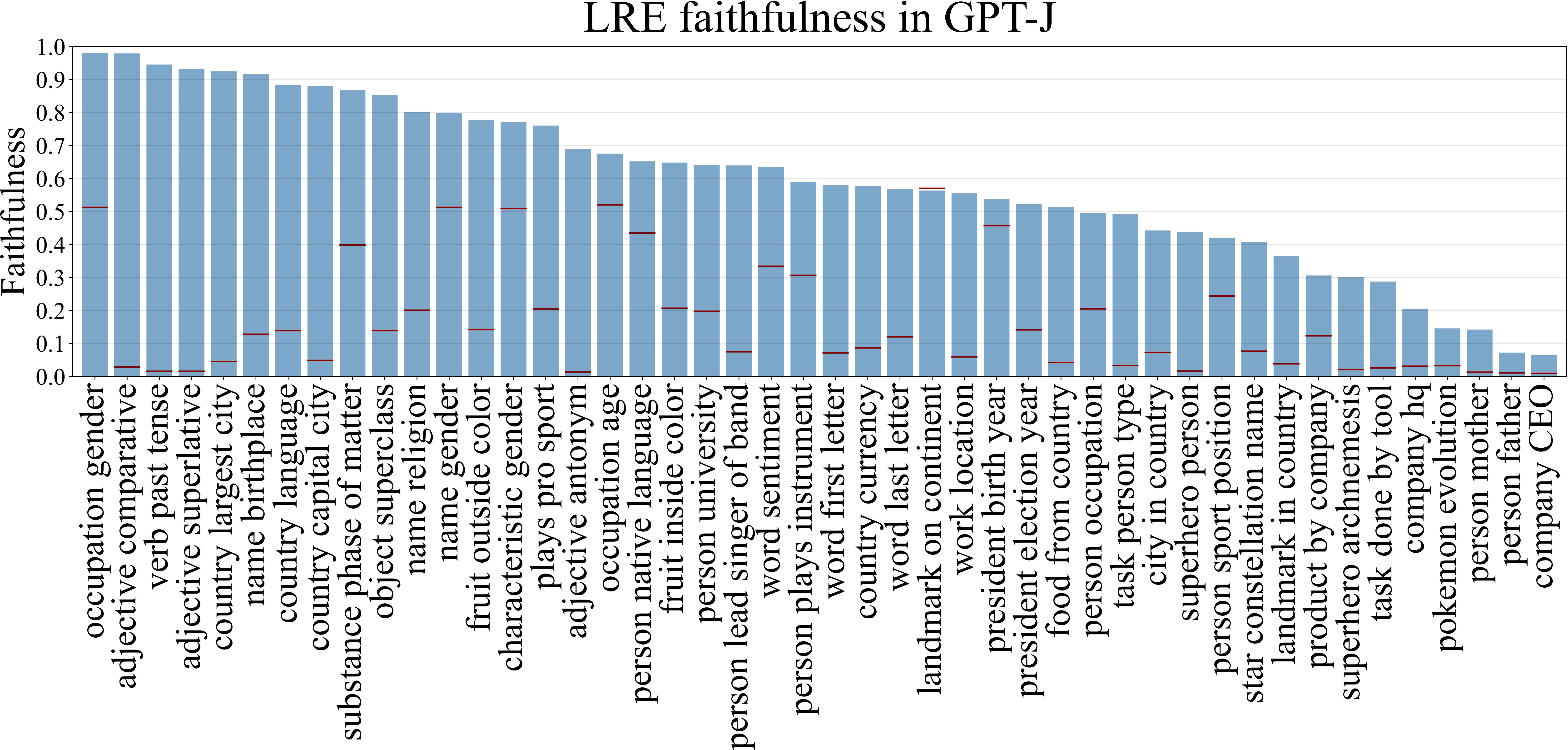
We evaluate the LRE approximations on a set of 47 relations spanning 4 categories: factual associations, commonsense knowledge, implicit biases, and linguistic knowledge. We find that for almost half of the relations LRE faithfully recovers subject-object mappings for a majority of the subjects in the test set.

We also identify a set of relations where we couldn't find a good LRE approximations. For most of these relations the range was names of people and companies. We think the range for this relations are so large that LM cannot encode them in a single state, and relies on a more complex non-linear decoding procedure.

Attribute Lens

Attribute Lens is motivated by the idea that a hidden state h may contain pieces of information beyond the prediction of the immediate next token. And, an LRE can be used to extract a certain attribute from h without relevant textual context.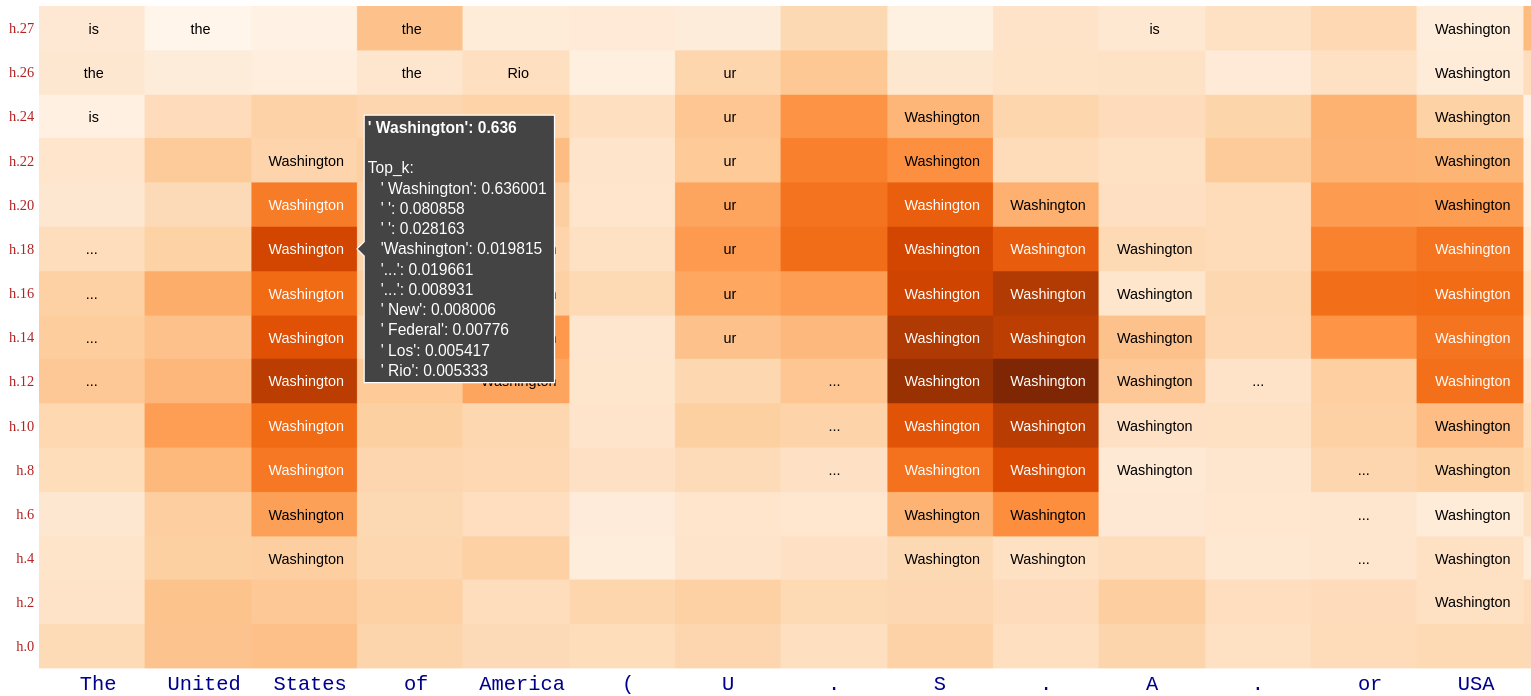
LRE approximating the relation country capital applied on hidden state h after different layers in different token positions.

How to cite

This work is not yet peer-reviewed. The preprint can be cited as follows.

bibliography

Evan Hernandez, Arnab Sen Sharma, Tal Haklay, Kevin Meng, Martin Wattenberg, Yonatan Belinkov, and David Bau. "Linearity of Relation Decoding in Transformer Language Models." Proceedings of the 2024 International Conference on Learning Representations. (ICLR 2024 spotlight)

bibtex

@inproceedings{hernandez2024linearity,
    title={Linearity of Relation Decoding in Transformer Language Models}, 
    author={Evan Hernandez and Arnab Sen Sharma and Tal Haklay and Kevin Meng and Martin Wattenberg and Jacob Andreas and Yonatan Belinkov and David Bau},
    booktitle={Proceedings of the 2024 International Conference on Learning Representations},
    year={2024},
}